圓柱斜齒齒輪在成形磨齒齒向修形加工過程中,會產生齒面扭曲,通過調整砂輪或優化多軸附加運動可以補償齒面扭曲,但齒面精度難以達到使用要求。
據此,提出了一種基于齒向修形曲線反向補償齒面扭曲的方法,利用實際修形曲線構造的虛擬齒面下的砂輪廓形反求修形齒面,以齒面扭曲評價指標為依據,分析得到補償后的最優砂輪廓形。
最后,以一斜齒輪鼓形修形為例利用VERICUT進行仿真分析,并根據實際齒面與理論齒面間的偏差量,計算齒面扭曲量。結果表明,基于反向補償思想補償齒面扭曲,可以有效消減齒面扭曲,提高齒輪齒向修形精度。
在齒輪生產過程中,齒向修形可以改善齒輪傳動過程中載荷分布不均勻的現象,提高齒輪承載能力,HAO等采用有限元法分析了齒向修形對齒輪傳動系統的影響,證明了齒向修形可以改善齒輪傳動系統的動態特性;
LIU等利用三維接觸有限元模型,驗證了通過齒向修形可以有效改善部分載荷和應力集中現象。但斜齒輪齒向修形過程中存在的齒面扭曲導致修形后的斜齒輪齒面精度降低,與理論要求的修形齒面差異大。
目前,國內外學者對針對齒面扭曲消減進行了大量的研究,張鑫等聯合蒙特卡洛法對修形前后的齒輪進行了接觸線優化,通過有限元算法分析了齒面扭曲對傳統誤差、齒面接觸應力的影響;
韓飛龍等通過分析齒面的嚙合跡線分布規律,得到了齒面偏差與砂輪位置變化規律;
唐永忠等針對齒面誤差、機床加工誤差,提出了一種基于最小二乘法的五軸聯動數控機床加工誤差補償方法;
李彥等提出了以砂輪安裝角為變量的多目標接觸線優化數學模型,采用貝葉斯BP神經網絡求解,以求得改善齒面扭曲后的最優齒向修形結果;
孫小敏等對運動多項式系數對齒面精度的影響進行敏感性分析,簡化了磨齒五軸運動多項式,為齒面誤差補償算法應用提供理論依據;
田曉青等提出了一種基于柔性電子齒輪箱多軸同步附加運動的齒面扭曲補償方法; ZHANG等通過分析齒輪參數對齒面扭曲的影響,并利用正交實驗驗證了齒輪參數對齒面扭曲的影響,其中模數變化對齒面扭曲影響最大;
TIAN等針對齒面扭曲問題,提出了一種基于遺傳算法的連續接觸線評估方法對齒面扭曲進行拓撲修正;
ZHAO等利用三維測量技術,獲取齒面扭曲偏差數據,并提出了一種基于正交多項式的齒面扭曲表達方法,并成功預測加工過程中的齒面扭曲程度。
目前,針對齒面扭曲消減方法主要是優化砂輪、增加機床附加運動量、優化修形曲線。具有代表性的格里森磨齒機就是采用反扭曲思想對齒面扭曲進行補償,這種方法對于齒面扭曲消減的效果顯著;
但目前國內對于利用上述思想反向補償齒輪磨削產生的齒面扭曲誤差的研究很少; 這種方法在國內具有一定的實用性和較高的創新性。
基于此,本文根據實際齒向修形曲線與理論修形齒面之間的關系,建立了虛擬齒面模型,提出一種基于齒向修形曲線構造虛擬齒面以反向補償齒面扭曲的方法,研究結果將為進一步消減齒面扭曲提供了新的解決思路。
成形磨齒坐標系建立:
五軸數控成形磨齒機一般主要包括X、Y、Z三個直線軸和A、C兩個旋轉軸。根據五軸聯動的數控成形磨齒機,建立數控成形磨齒空間嚙合坐標系如圖1所示。
其中坐標系Og-XgYgZg和齒輪固聯,坐標系Ow-XwYwZw分別與和砂輪固聯。其中砂輪與齒輪之間的中心距為a,砂輪安裝角(即Zg與Zw之間的夾角)為Σ。
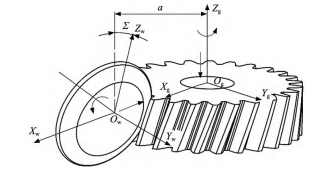
圖1 成形磨齒空間嚙合坐標系
則根據齊次坐標變換原理,可以得到砂輪坐標系Ow-XwYwZw與齒輪坐標系Og-XgYgZg之間的變換關系為:
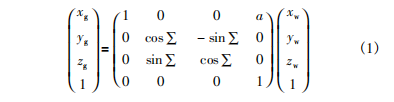
齒向修形建模:
磨齒加工過程中,齒向修形通常是采用齒端修形、鼓形修形以及螺旋角修形3種修形方式。本文以鼓形齒向修形為例,對斜齒輪齒向修形過程中產生的齒面扭曲進行分析研究。
圖2為鼓形修形示意圖,齒寬為b,鼓形修形量為δ。鼓形修形曲線采用拋物線型,記為H(z)。齒寬中部修形量最小,齒寬兩端處修形量最大。
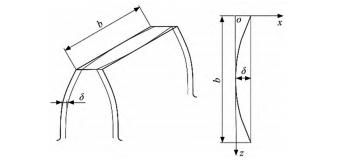
圖2 鼓形修形示意圖
齒向修形之后,端截面的齒廓位置將會發生改變,將修形后的廓形可以看作是標準的齒廓廓形繞分度圓圓心旋轉一個附加轉角γ之后得到的。如圖3所示。
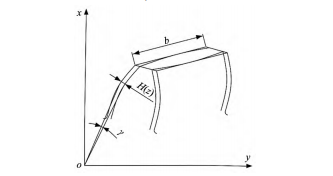
圖3 修形曲線的疊加
附加轉角γ與修形函數H(z)之間的關系為:

式中: r為分度圓半徑,β為斜齒輪螺旋角。
則將該附加轉角疊加進標準的螺旋運動后可以得到如下的理論齒向修形齒面方程:
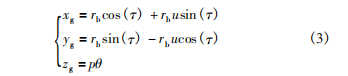
式中: τ=u+σb+θ+γ,rb為基圓半徑,p為螺旋參數,σb為齒輪基圓齒槽半角,u、θ為漸開線參數。
在進行鼓形齒向修形時,理論上是要求齒面兩端修形量對稱分布且完全相等,但在修形斜齒輪時,因齒向不同截面的修形量不同和空間接觸線的扭曲異變,會導致齒向修形齒面產生齒面扭曲現象。
以同一齒寬處齒頂圓的齒向修形量與齒根圓處的齒向修形量之間的偏差值來判斷齒面扭曲的大小,記該值為齒面偏差量ec,作為齒面扭曲評價指標,如圖4所示。
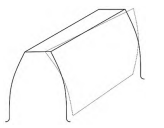
圖4 齒面扭曲現象
圖5為斜齒輪齒面展開平面圖,圖中的AB、CD、EF三條線為齒向修形過程中的齒輪與砂輪之間的接觸線。軸截面AF上的齒面偏差量可以看作是接觸線EF上的齒頂圓修形量與接觸線AB上的齒根圓修形量之差。
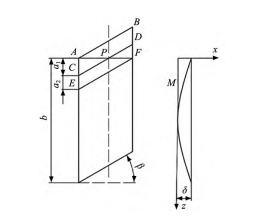
圖5 齒面展開平面
建立如圖5中所示的坐標系XOZ,鼓形修形曲線為H(z),記上圖中AC=a1,CE=a2。
設上圖中軸截面AF處橫坐標為z=h,則圖5中軸截面AF上的齒面偏差量ec的表達式為:

利用齒面反扭曲思想,根據實際齒向修形曲線與理論齒向修形曲線之間的偏差值,設計一虛擬齒向修形曲面,并以k1、k2作為補償量值。
以齒面偏差量ec最小為目標,以k1、k2為變量,利用動態慣性權重的微粒群優化算法求解最優的k1、k2。
齒向修形反向補償分析流程圖如圖6所示。
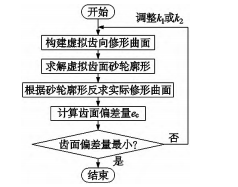
圖6 補償流程圖
反向補償齒向修形建模:
對實際齒向修形曲線進行偏移(或旋轉),構造虛擬齒向修形曲面。圖7為實際修形曲線與偏移后修形曲線。
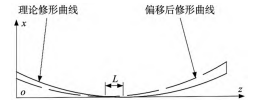
圖7 修形曲線偏移
圖8為實際修形曲線與旋轉后修形曲線。
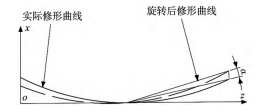
圖8 修行曲線旋轉
則偏移(或旋轉)后的不同齒高處的齒向修形曲線方程為:
 L與漸開線齒廓上任意一點的半徑ri的關系為:
L與漸開線齒廓上任意一點的半徑ri的關系為:
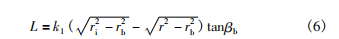
α與漸開線齒廓上任意一點的半徑ri的關系為:
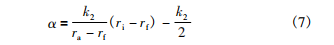
式中: ri=rb/cos(arctanu),βb為基圓螺旋角,ra為齒頂圓圓半徑,rf為齒根圓半徑,k1取值范圍為[0,1],k2取值范圍為[0,0.5]。
則由實際修形曲線偏移(或旋轉)后的修形曲面與理論齒向修形曲面之間的關系,可得構造的虛擬齒向修形齒面與理論修形齒面間的坐標變換關系為:
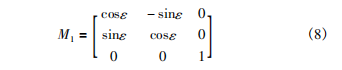
式中: ε=(H(z)-H1(z))/ri。
則聯立式(8)與式(3)可得虛擬齒向修形齒面方程為:
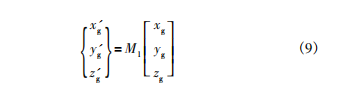
反向補償齒向修形砂輪廓形求解:
根據成形磨削時砂輪與齒輪的相對運動速度與齒面法向量垂直這一條件,即v·n=0,可以得到砂輪面上的接觸條件式。
由式(9)可以求得虛擬齒向齒面上的法向量:
 式中: r=x'gi+y'gj+z'gk。
式中: r=x'gi+y'gj+z'gk。
由此可以推導出虛擬齒面與砂輪間的接觸線條件式為:
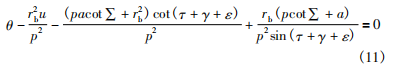
上述條件式為超越方程,故采用牛頓迭代法對其進行求解,令u在值域內變化獲得一系列的離散值,在帶入式(11)求解對應的θ值,后將求得的(u,θ) 帶入砂輪坐標系下的齒面方程可以得到該虛擬齒面下(即補償后)的砂輪接觸線。
將該接觸線繞砂輪軸線回轉即可得到補償后砂輪回轉面。將接觸線投影到砂輪計算平面就可以得到補償后的砂輪廓形。砂輪軸向截形數學表達式為:
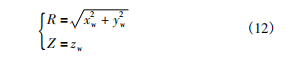
基于補償的砂輪廓形反求齒面:
圖9為砂輪廓形曲線。
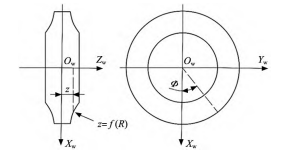
圖9 砂輪廓形
如圖9所示,在砂輪坐標系Ow-XwYwZw下建立如下砂輪回轉面方程:
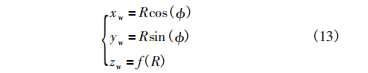
式中: R為砂輪截形上任意點的半徑,φ為砂輪回轉角度,f(R)為砂輪廓形方程式。
根據成形磨削時砂輪與齒輪的相對運動速度與砂輪面法向量垂直這一條件,即v·n1=0,可以得到齒面上的接觸條件式。則其中n1可以由補償后的砂輪面方程求偏導得到。
由此可以推導出補償后的砂輪與齒面間的接觸線條件式為:

式(14)亦為超越方程,采用同式(11)同樣的求解方法,將求得的齒面接觸線繞齒輪軸線做螺旋運動即可得到如下補償后齒向修形齒面方程。
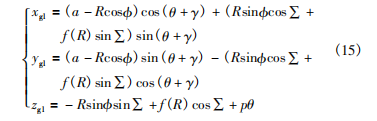
本文選取齒輪及鼓形量參數如表1所示。
通過對補償后的砂輪廓形導入VERICUT中進行仿真,并與理論齒向修形齒面進行比較。
圖10為未補償時實際修形與理論修形齒面對比圖。

圖10 實際修形與理論修形齒面對比圖
修形曲線偏移:
圖11為根據上述流程圖7由實際齒向修形曲面偏移補償后得到的砂輪廓形與理論砂輪廓形對比。
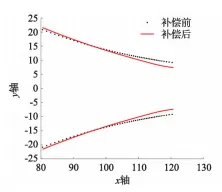
圖11 偏移補償砂輪廓形對比
圖12為修形曲線偏移補償后實際修形與理論修形齒面對比圖。

圖12 偏移補償后實際修形與理論修形對比圖
圖13為補償前后與理論齒面偏差距離對比圖。
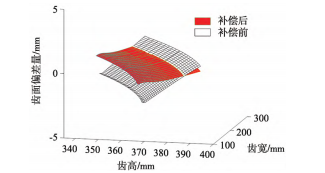
圖13 補償前后與理論齒面偏差距離對比圖
從圖13中可以看出補償后齒面距離理論齒面的偏差距離明顯減小。表2為補償前齒向修形后實際曲面與理論修形曲面間的偏差值,從中可以得到在未進行補償時,修形齒面與理論齒面間偏差值在[-2,2]mm之間,變化值為4mm。
通過對表2中數據的整理計算可以得到在未補償時齒頂和齒根修形量差值最大為3.02mm。
從表3中可以得到,在進行補償后,修形齒面與理論齒面間偏差距離在[-0.5,1.5]mm之間,變化值為2mm。
通過對表3數據的整理計算可以得到在未補償時齒頂和齒根修形量差值最大為1.32mm。可以看出齒面扭曲明顯減小,修形量偏差值減小56% 。
圖14為根據上述流程圖6由實際齒向修形曲面旋轉補償后得到的砂輪廓形與理論砂輪廓形對比。
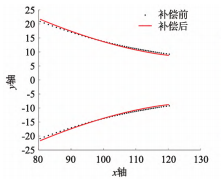
圖14 曲線旋轉補償砂輪廓形對比
圖15為修形曲線旋轉補償后實際修形與理論修形齒面對比圖。
圖15旋轉補償后實際修形與理論修形對比
根據修形曲線旋轉得到的虛擬齒向修形曲面,補償后得到調整過的砂輪廓形。針對補償后的砂輪廓形對修形齒面進行仿真,并與理論齒面進行比較,可以得到如表4中的數據,在進行補償后,修形齒面與理論齒面間偏差距離在[-1.9,1.7]之間,變化值為3.6mm。圖16為補償前后與理論齒面偏差距離對比圖。
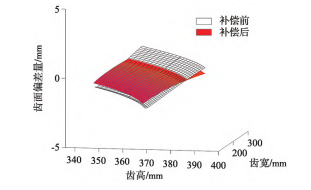
圖16 補償前后與理論齒面偏差距離對比圖
通過對表4數據的整理、計算可以得到在未補償時齒頂和齒根修形量差值最大為2.3mm。可以看出齒面扭曲減小,修形量偏差值減小23.3% 。
仿真結果表明,通過旋轉或者偏移實際齒向修形曲線構造虛擬齒向修形曲面,在反求修整后的砂輪廓形,都可以減小齒面扭曲誤差。
其中偏移實際齒向修形曲線構造虛擬修形齒面,可以使得齒面扭曲減小56%,有效改善了成形磨削斜齒輪過程中的齒向修形扭曲誤差,驗證了文中提出方法的有效性。

圖17 成形磨齒加工試驗
實驗所選取的齒輪及鼓形量參數如表1所示,通過以上齒面扭曲反向補償方法,獲得補償前后的齒面扭曲偏差量ec,如表5所示。
由表5可知,齒面扭曲偏差量作為衡量齒面扭曲的指標,在該成形磨齒實驗中,齒面扭曲明顯減小,經補償后,齒面扭曲減小了54%。
通過分析砂輪廓形和齒輪齒面之間的關系,提出了基于實際齒向修形曲線構造虛擬齒向修形齒面反向補償齒面扭曲的方法,得到如下結論:
(1) 在數控成形磨齒齒向修形過程中,齒向修形曲面產生扭曲的原因為實際修形曲線的偏移,因此從實際修形曲線偏移角度出發,構造虛擬齒面,補償齒面扭曲。
(2) 齒面扭曲的補償實例表明,通過偏移實際齒向修形曲面構造虛擬齒向修形曲面,反求補償后的砂輪廓形的補償方法可以使得齒面扭曲減小54%。
綜上所述,本文從齒面反扭曲思想出發反向補償齒輪,并提出了一種全新的齒面扭曲消減方法,最終實現對齒面扭曲有效的消減。
研究結果表明相較于傳統的齒面扭曲消減方法,此方法可以明顯降低齒面扭曲量,并為后續齒面扭曲消減提供了一種實用、創新的思路。
參考文獻:略
作者簡介: 沈敏(1999—),女,碩士研究生,研究方向為機械設計及其自動化。
據此,提出了一種基于齒向修形曲線反向補償齒面扭曲的方法,利用實際修形曲線構造的虛擬齒面下的砂輪廓形反求修形齒面,以齒面扭曲評價指標為依據,分析得到補償后的最優砂輪廓形。
最后,以一斜齒輪鼓形修形為例利用VERICUT進行仿真分析,并根據實際齒面與理論齒面間的偏差量,計算齒面扭曲量。結果表明,基于反向補償思想補償齒面扭曲,可以有效消減齒面扭曲,提高齒輪齒向修形精度。
引 言
在齒輪生產過程中,齒向修形可以改善齒輪傳動過程中載荷分布不均勻的現象,提高齒輪承載能力,HAO等采用有限元法分析了齒向修形對齒輪傳動系統的影響,證明了齒向修形可以改善齒輪傳動系統的動態特性;
LIU等利用三維接觸有限元模型,驗證了通過齒向修形可以有效改善部分載荷和應力集中現象。但斜齒輪齒向修形過程中存在的齒面扭曲導致修形后的斜齒輪齒面精度降低,與理論要求的修形齒面差異大。
目前,國內外學者對針對齒面扭曲消減進行了大量的研究,張鑫等聯合蒙特卡洛法對修形前后的齒輪進行了接觸線優化,通過有限元算法分析了齒面扭曲對傳統誤差、齒面接觸應力的影響;
韓飛龍等通過分析齒面的嚙合跡線分布規律,得到了齒面偏差與砂輪位置變化規律;
唐永忠等針對齒面誤差、機床加工誤差,提出了一種基于最小二乘法的五軸聯動數控機床加工誤差補償方法;
李彥等提出了以砂輪安裝角為變量的多目標接觸線優化數學模型,采用貝葉斯BP神經網絡求解,以求得改善齒面扭曲后的最優齒向修形結果;
孫小敏等對運動多項式系數對齒面精度的影響進行敏感性分析,簡化了磨齒五軸運動多項式,為齒面誤差補償算法應用提供理論依據;
田曉青等提出了一種基于柔性電子齒輪箱多軸同步附加運動的齒面扭曲補償方法; ZHANG等通過分析齒輪參數對齒面扭曲的影響,并利用正交實驗驗證了齒輪參數對齒面扭曲的影響,其中模數變化對齒面扭曲影響最大;
TIAN等針對齒面扭曲問題,提出了一種基于遺傳算法的連續接觸線評估方法對齒面扭曲進行拓撲修正;
ZHAO等利用三維測量技術,獲取齒面扭曲偏差數據,并提出了一種基于正交多項式的齒面扭曲表達方法,并成功預測加工過程中的齒面扭曲程度。
目前,針對齒面扭曲消減方法主要是優化砂輪、增加機床附加運動量、優化修形曲線。具有代表性的格里森磨齒機就是采用反扭曲思想對齒面扭曲進行補償,這種方法對于齒面扭曲消減的效果顯著;
但目前國內對于利用上述思想反向補償齒輪磨削產生的齒面扭曲誤差的研究很少; 這種方法在國內具有一定的實用性和較高的創新性。
基于此,本文根據實際齒向修形曲線與理論修形齒面之間的關系,建立了虛擬齒面模型,提出一種基于齒向修形曲線構造虛擬齒面以反向補償齒面扭曲的方法,研究結果將為進一步消減齒面扭曲提供了新的解決思路。
成形磨齒齒向修形齒面分析
成形磨齒坐標系建立:
五軸數控成形磨齒機一般主要包括X、Y、Z三個直線軸和A、C兩個旋轉軸。根據五軸聯動的數控成形磨齒機,建立數控成形磨齒空間嚙合坐標系如圖1所示。
其中坐標系Og-XgYgZg和齒輪固聯,坐標系Ow-XwYwZw分別與和砂輪固聯。其中砂輪與齒輪之間的中心距為a,砂輪安裝角(即Zg與Zw之間的夾角)為Σ。

圖1 成形磨齒空間嚙合坐標系
則根據齊次坐標變換原理,可以得到砂輪坐標系Ow-XwYwZw與齒輪坐標系Og-XgYgZg之間的變換關系為:
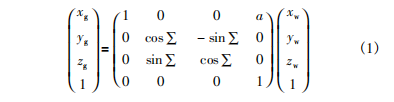
磨齒加工過程中,齒向修形通常是采用齒端修形、鼓形修形以及螺旋角修形3種修形方式。本文以鼓形齒向修形為例,對斜齒輪齒向修形過程中產生的齒面扭曲進行分析研究。
圖2為鼓形修形示意圖,齒寬為b,鼓形修形量為δ。鼓形修形曲線采用拋物線型,記為H(z)。齒寬中部修形量最小,齒寬兩端處修形量最大。

圖2 鼓形修形示意圖

圖3 修形曲線的疊加
附加轉角γ與修形函數H(z)之間的關系為:
式中: r為分度圓半徑,β為斜齒輪螺旋角。
則將該附加轉角疊加進標準的螺旋運動后可以得到如下的理論齒向修形齒面方程:
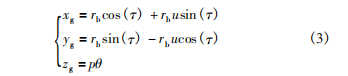
齒向修形齒面扭曲分析
在進行鼓形齒向修形時,理論上是要求齒面兩端修形量對稱分布且完全相等,但在修形斜齒輪時,因齒向不同截面的修形量不同和空間接觸線的扭曲異變,會導致齒向修形齒面產生齒面扭曲現象。
以同一齒寬處齒頂圓的齒向修形量與齒根圓處的齒向修形量之間的偏差值來判斷齒面扭曲的大小,記該值為齒面偏差量ec,作為齒面扭曲評價指標,如圖4所示。

圖4 齒面扭曲現象
圖5為斜齒輪齒面展開平面圖,圖中的AB、CD、EF三條線為齒向修形過程中的齒輪與砂輪之間的接觸線。軸截面AF上的齒面偏差量可以看作是接觸線EF上的齒頂圓修形量與接觸線AB上的齒根圓修形量之差。

圖5 齒面展開平面
建立如圖5中所示的坐標系XOZ,鼓形修形曲線為H(z),記上圖中AC=a1,CE=a2。
設上圖中軸截面AF處橫坐標為z=h,則圖5中軸截面AF上的齒面偏差量ec的表達式為:
基于修形曲線的齒面扭曲反向補償方法
利用齒面反扭曲思想,根據實際齒向修形曲線與理論齒向修形曲線之間的偏差值,設計一虛擬齒向修形曲面,并以k1、k2作為補償量值。
以齒面偏差量ec最小為目標,以k1、k2為變量,利用動態慣性權重的微粒群優化算法求解最優的k1、k2。
齒向修形反向補償分析流程圖如圖6所示。

圖6 補償流程圖
反向補償齒向修形建模:
對實際齒向修形曲線進行偏移(或旋轉),構造虛擬齒向修形曲面。圖7為實際修形曲線與偏移后修形曲線。

圖7 修形曲線偏移
圖8為實際修形曲線與旋轉后修形曲線。

圖8 修行曲線旋轉
則偏移(或旋轉)后的不同齒高處的齒向修形曲線方程為:
α與漸開線齒廓上任意一點的半徑ri的關系為:
則由實際修形曲線偏移(或旋轉)后的修形曲面與理論齒向修形曲面之間的關系,可得構造的虛擬齒向修形齒面與理論修形齒面間的坐標變換關系為:
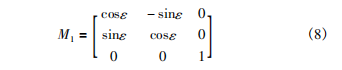
則聯立式(8)與式(3)可得虛擬齒向修形齒面方程為:
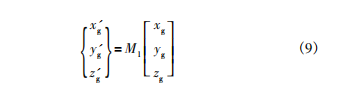
反向補償齒向修形砂輪廓形求解:
根據成形磨削時砂輪與齒輪的相對運動速度與齒面法向量垂直這一條件,即v·n=0,可以得到砂輪面上的接觸條件式。
由式(9)可以求得虛擬齒向齒面上的法向量:
由此可以推導出虛擬齒面與砂輪間的接觸線條件式為:
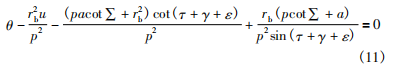
將該接觸線繞砂輪軸線回轉即可得到補償后砂輪回轉面。將接觸線投影到砂輪計算平面就可以得到補償后的砂輪廓形。砂輪軸向截形數學表達式為:
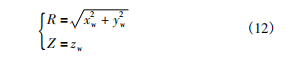
基于補償的砂輪廓形反求齒面:
圖9為砂輪廓形曲線。

圖9 砂輪廓形
如圖9所示,在砂輪坐標系Ow-XwYwZw下建立如下砂輪回轉面方程:
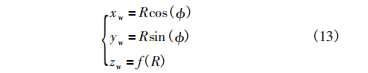
式中: R為砂輪截形上任意點的半徑,φ為砂輪回轉角度,f(R)為砂輪廓形方程式。
根據成形磨削時砂輪與齒輪的相對運動速度與砂輪面法向量垂直這一條件,即v·n1=0,可以得到齒面上的接觸條件式。則其中n1可以由補償后的砂輪面方程求偏導得到。
由此可以推導出補償后的砂輪與齒面間的接觸線條件式為:

式(14)亦為超越方程,采用同式(11)同樣的求解方法,將求得的齒面接觸線繞齒輪軸線做螺旋運動即可得到如下補償后齒向修形齒面方程。
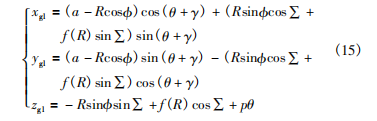
實例分析
本文選取齒輪及鼓形量參數如表1所示。
表1 齒輪參數


通過對補償后的砂輪廓形導入VERICUT中進行仿真,并與理論齒向修形齒面進行比較。
圖10為未補償時實際修形與理論修形齒面對比圖。

圖10 實際修形與理論修形齒面對比圖
修形曲線偏移:
圖11為根據上述流程圖7由實際齒向修形曲面偏移補償后得到的砂輪廓形與理論砂輪廓形對比。

圖11 偏移補償砂輪廓形對比
圖12為修形曲線偏移補償后實際修形與理論修形齒面對比圖。

圖12 偏移補償后實際修形與理論修形對比圖
圖13為補償前后與理論齒面偏差距離對比圖。

圖13 補償前后與理論齒面偏差距離對比圖
從圖13中可以看出補償后齒面距離理論齒面的偏差距離明顯減小。表2為補償前齒向修形后實際曲面與理論修形曲面間的偏差值,從中可以得到在未進行補償時,修形齒面與理論齒面間偏差值在[-2,2]mm之間,變化值為4mm。
通過對表2中數據的整理計算可以得到在未補償時齒頂和齒根修形量差值最大為3.02mm。
表2 補償前與理論齒面間偏差數據


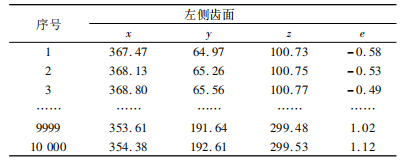
從表3中可以得到,在進行補償后,修形齒面與理論齒面間偏差距離在[-0.5,1.5]mm之間,變化值為2mm。
通過對表3數據的整理計算可以得到在未補償時齒頂和齒根修形量差值最大為1.32mm。可以看出齒面扭曲明顯減小,修形量偏差值減小56% 。
表3 補償后與理論齒面間偏差數據
修形曲線旋轉:
圖14為根據上述流程圖6由實際齒向修形曲面旋轉補償后得到的砂輪廓形與理論砂輪廓形對比。

圖14 曲線旋轉補償砂輪廓形對比
圖15為修形曲線旋轉補償后實際修形與理論修形齒面對比圖。

圖15旋轉補償后實際修形與理論修形對比
根據修形曲線旋轉得到的虛擬齒向修形曲面,補償后得到調整過的砂輪廓形。針對補償后的砂輪廓形對修形齒面進行仿真,并與理論齒面進行比較,可以得到如表4中的數據,在進行補償后,修形齒面與理論齒面間偏差距離在[-1.9,1.7]之間,變化值為3.6mm。圖16為補償前后與理論齒面偏差距離對比圖。

圖16 補償前后與理論齒面偏差距離對比圖
通過對表4數據的整理、計算可以得到在未補償時齒頂和齒根修形量差值最大為2.3mm。可以看出齒面扭曲減小,修形量偏差值減小23.3% 。
表4 補償后與理論齒面間偏差數據


仿真結果表明,通過旋轉或者偏移實際齒向修形曲線構造虛擬齒向修形曲面,在反求修整后的砂輪廓形,都可以減小齒面扭曲誤差。
其中偏移實際齒向修形曲線構造虛擬修形齒面,可以使得齒面扭曲減小56%,有效改善了成形磨削斜齒輪過程中的齒向修形扭曲誤差,驗證了文中提出方法的有效性。
磨齒加工試驗驗證
基于齒面扭曲反向補償方法,并采用基于X、Z、C三軸徑向極坐標法進行測量,來驗證虛擬齒面補償方法的實用性和準確性。成形磨齒齒向修形加工試驗如圖17所示。
圖17 成形磨齒加工試驗
實驗所選取的齒輪及鼓形量參數如表1所示,通過以上齒面扭曲反向補償方法,獲得補償前后的齒面扭曲偏差量ec,如表5所示。
由表5可知,齒面扭曲偏差量作為衡量齒面扭曲的指標,在該成形磨齒實驗中,齒面扭曲明顯減小,經補償后,齒面扭曲減小了54%。
表5 補償前后齒面扭曲偏差量測量結果


結 論
通過分析砂輪廓形和齒輪齒面之間的關系,提出了基于實際齒向修形曲線構造虛擬齒向修形齒面反向補償齒面扭曲的方法,得到如下結論:
(1) 在數控成形磨齒齒向修形過程中,齒向修形曲面產生扭曲的原因為實際修形曲線的偏移,因此從實際修形曲線偏移角度出發,構造虛擬齒面,補償齒面扭曲。
(2) 齒面扭曲的補償實例表明,通過偏移實際齒向修形曲面構造虛擬齒向修形曲面,反求補償后的砂輪廓形的補償方法可以使得齒面扭曲減小54%。
綜上所述,本文從齒面反扭曲思想出發反向補償齒輪,并提出了一種全新的齒面扭曲消減方法,最終實現對齒面扭曲有效的消減。
研究結果表明相較于傳統的齒面扭曲消減方法,此方法可以明顯降低齒面扭曲量,并為后續齒面扭曲消減提供了一種實用、創新的思路。
參考文獻:略
作者簡介: 沈敏(1999—),女,碩士研究生,研究方向為機械設計及其自動化。
