編者按:
各位粉絲朋友們,歡迎閱讀本期小編推送的《汽車驅動橋螺旋錐齒輪齒面測量誤差補償方法》文章。文章主要介紹了提升汽車驅動橋螺旋錐齒輪齒面加工質量對整車的安全與節能性能有重要意義。
該文針對汽車驅動橋螺旋錐齒輪實測和理論齒面存在的測量誤差,提出了一種基于對偶四元數優化的迭代最近點(ICP)齒面測量誤差補償方法。
本篇文章因篇幅較長,特安排兩期推送,本期推出文章最后剩余內容。
本期推出:汽車驅動橋螺旋錐齒輪齒面測量誤差補償方法(二)
為了驗證本文算法的補償效果,使用如圖6所示HyB-35型齒輪測量機對汽車驅動橋螺旋錐齒輪齒面進行點接觸式測量。
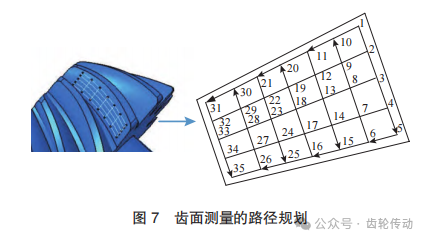
 螺旋錐齒輪齒面方程是超越非線性方程,為了讓測量結果盡可能全面地反映實測齒面的形貌信息,對螺旋錐齒輪的齒面進行測量時,通常在軸截面上進行網格規劃。根據螺旋錐齒輪的齒面構造和螺旋線走向, 保證檢測路徑最短且不發生碰撞,本文將小齒輪凹齒面進行網格化,劃分為5×7=35個點,由背錐向頂錐進行“ S”形測量方式獲得齒面測量點數據,如圖7所示。
螺旋錐齒輪齒面方程是超越非線性方程,為了讓測量結果盡可能全面地反映實測齒面的形貌信息,對螺旋錐齒輪的齒面進行測量時,通常在軸截面上進行網格規劃。根據螺旋錐齒輪的齒面構造和螺旋線走向, 保證檢測路徑最短且不發生碰撞,本文將小齒輪凹齒面進行網格化,劃分為5×7=35個點,由背錐向頂錐進行“ S”形測量方式獲得齒面測量點數據,如圖7所示。
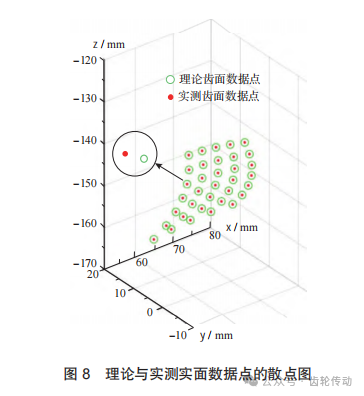
 根據圖7確定的測量路徑對螺旋錐齒輪齒面進行測量,獲得實測點齒面坐標點集Q。在MATLAB2020軟件中繪制理論測量點集P與實際測量點集Q的空間散點圖如圖8所示。由于誤差較小,在三維坐標下看不到全齒面的對應關系,將其局部對應點進行放大展示。其中空心點代表理論測量點,實心點代表實際測量點。
根據圖7確定的測量路徑對螺旋錐齒輪齒面進行測量,獲得實測點齒面坐標點集Q。在MATLAB2020軟件中繪制理論測量點集P與實際測量點集Q的空間散點圖如圖8所示。由于誤差較小,在三維坐標下看不到全齒面的對應關系,將其局部對應點進行放大展示。其中空心點代表理論測量點,實心點代表實際測量點。
 本實驗點云規模小,在該模型中采用定向對應點, 引入權重系數k,可以有效避免錯誤對應點的產生。利用本文提出的基于對偶四元數優化的ICP迭代算法誤差補償模型對上述齒面實測數據與理論數據之間的偏差進行補償,將得到的結果分別與基于SVD分解法、四元數法和L-M法的粗配準結果進行對比,并以對應點間歐氏距離作為評定標準。由實測數據計算出初始平均誤差為10.34μm,初始平均誤差最大誤差為22.11μm,然后對各算法誤差補償效果進行評估。 各算法的粗配準結果如圖9所示,由圖可知,4種算法經過粗配準后都更靠近零刻線,且SVD法和四元數法進行粗配準的誤差補償效果相差不大,L-M法的x軸方向補償后誤差值與理想坐標偏離較大,本文算法補償后坐標值與理想坐標值之差與其他3種算法相比更靠近零刻線。證明在粗配準階段本文算法補償效果為4種算法中最佳。
本實驗點云規模小,在該模型中采用定向對應點, 引入權重系數k,可以有效避免錯誤對應點的產生。利用本文提出的基于對偶四元數優化的ICP迭代算法誤差補償模型對上述齒面實測數據與理論數據之間的偏差進行補償,將得到的結果分別與基于SVD分解法、四元數法和L-M法的粗配準結果進行對比,并以對應點間歐氏距離作為評定標準。由實測數據計算出初始平均誤差為10.34μm,初始平均誤差最大誤差為22.11μm,然后對各算法誤差補償效果進行評估。 各算法的粗配準結果如圖9所示,由圖可知,4種算法經過粗配準后都更靠近零刻線,且SVD法和四元數法進行粗配準的誤差補償效果相差不大,L-M法的x軸方向補償后誤差值與理想坐標偏離較大,本文算法補償后坐標值與理想坐標值之差與其他3種算法相比更靠近零刻線。證明在粗配準階段本文算法補償效果為4種算法中最佳。
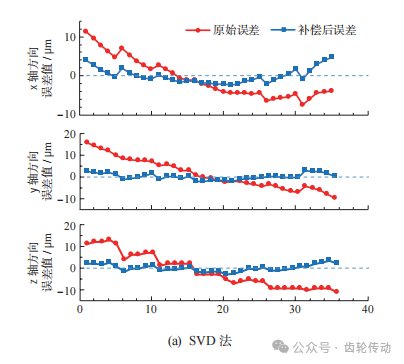
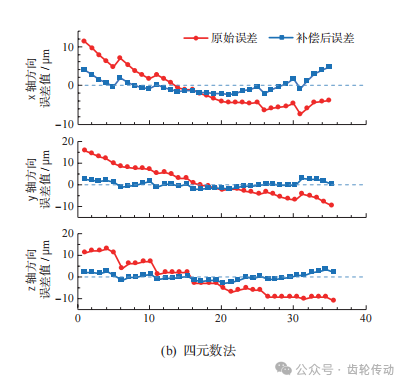
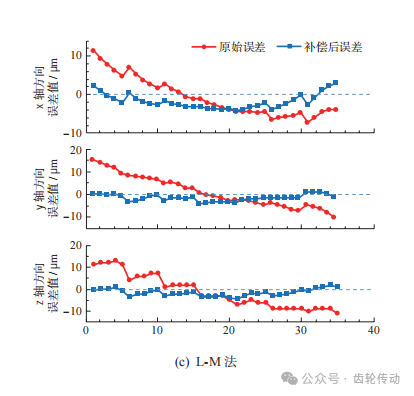
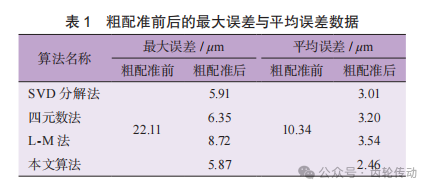
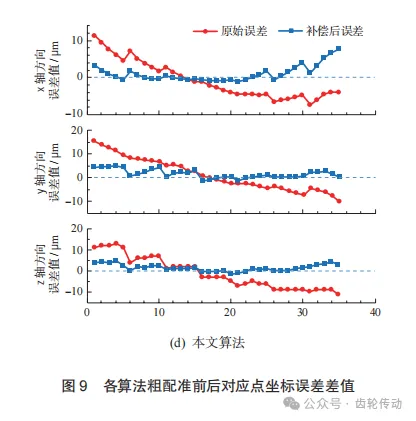 表1為粗配準前后的最大誤差與平均誤差數據。由表可知,4種算法的最大誤差分別降低了16.20、15.76、13.39和16.24μm,平均誤差分別降低了7.33、7.14、 6.80和7.88μm,本文算法相比于其他算法的結果更優。
表1為粗配準前后的最大誤差與平均誤差數據。由表可知,4種算法的最大誤差分別降低了16.20、15.76、13.39和16.24μm,平均誤差分別降低了7.33、7.14、 6.80和7.88μm,本文算法相比于其他算法的結果更優。
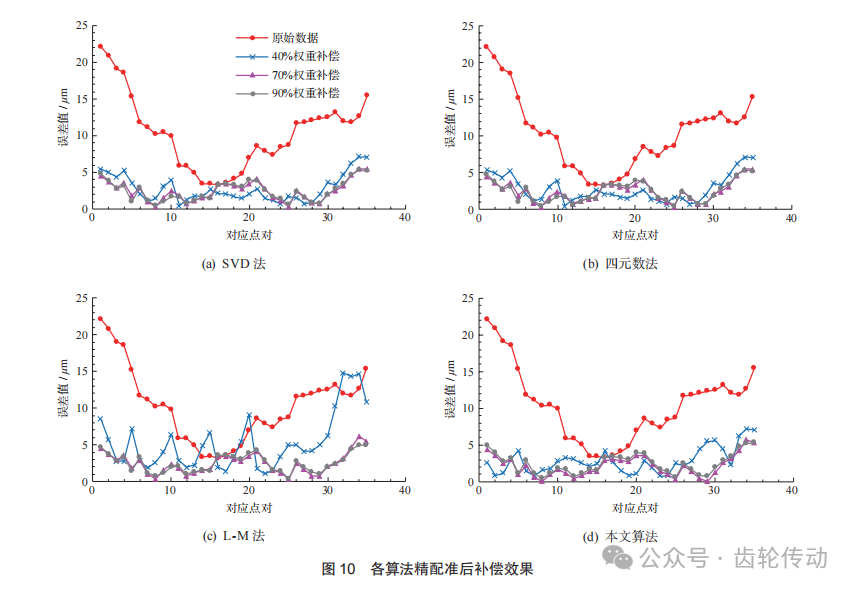
 在粗配準之后,將各算法獲取的配準參數值作為精配準的初始參數值。利用點到點 (point-to-point) ICP迭代算法進行精配準,各算法模型中權重k分別等于40%、70%和90%時的補償效果如圖10所示。由圖可知,在實驗的3組不同權重中,各類算法權重系數k=70%時誤差補償效果最佳,k=90%時次之,k=40%時較差。雖然SVD法、四元數法和L-M法對齒面誤差均有補償作用,但本文算法最終的補償效果更好,且最終誤差更小。
在粗配準之后,將各算法獲取的配準參數值作為精配準的初始參數值。利用點到點 (point-to-point) ICP迭代算法進行精配準,各算法模型中權重k分別等于40%、70%和90%時的補償效果如圖10所示。由圖可知,在實驗的3組不同權重中,各類算法權重系數k=70%時誤差補償效果最佳,k=90%時次之,k=40%時較差。雖然SVD法、四元數法和L-M法對齒面誤差均有補償作用,但本文算法最終的補償效果更好,且最終誤差更小。
 精配準后,將基于SVD法、四元數法、L-M法和本文算法進行配準的ICP迭代法的最終誤差補償結果進行分析,根據式(18)給出了各算法模型權重分別為40%、70%和90%時的誤差補償數據結果,并得出各算法10次獨立運算時間的均值,如表2所示。由表可得,各算法在權重k為70%時,補償效果最佳,且本文算法相較于SVD法、四元數法和L-M法進行ICP迭代補償后的最高誤差補償率分別提升了3.09%、3.10%和3.12%。權重k為70%時,在粗配準階段,SVD 法、 四元數法、L-M法和本文算法的最大誤差由補償前的22.11μm分別補償至 5.90、6.35、8.72 和5.87μm,再進一步進行精配準補償至5.67、5.79、6.38和5.64μm,測量齒面與理論齒面對應點平均誤差從10.34μm分別補償至2.71、2.70、2.70和2.38μm;本文算法相比于其他3種算法平均耗時增加了0.14、0.08和0.18s, 這是由于運行算法的過程中需要調用工具箱Sedumi求解。
精配準后,將基于SVD法、四元數法、L-M法和本文算法進行配準的ICP迭代法的最終誤差補償結果進行分析,根據式(18)給出了各算法模型權重分別為40%、70%和90%時的誤差補償數據結果,并得出各算法10次獨立運算時間的均值,如表2所示。由表可得,各算法在權重k為70%時,補償效果最佳,且本文算法相較于SVD法、四元數法和L-M法進行ICP迭代補償后的最高誤差補償率分別提升了3.09%、3.10%和3.12%。權重k為70%時,在粗配準階段,SVD 法、 四元數法、L-M法和本文算法的最大誤差由補償前的22.11μm分別補償至 5.90、6.35、8.72 和5.87μm,再進一步進行精配準補償至5.67、5.79、6.38和5.64μm,測量齒面與理論齒面對應點平均誤差從10.34μm分別補償至2.71、2.70、2.70和2.38μm;本文算法相比于其他3種算法平均耗時增加了0.14、0.08和0.18s, 這是由于運行算法的過程中需要調用工具箱Sedumi求解。
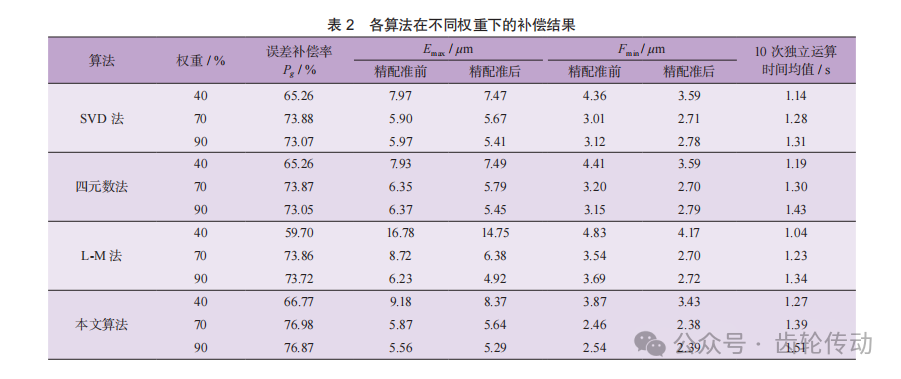 如圖11所示,將各算法在不同權重下的最終結果進行比較。由圖可知,各算法在權重為40%時,最大誤差及誤差補償率都較差,這是由于在權重為40%時, 選取的點不足以顯示全齒面的數據特征,導致一些齒面點的誤差不能進行精細的補償。而在權重為70%和90%時,各算法的最大誤差及誤差補償率相差不大,但70%更佳,這是由于在權重為90%時,雖然幾乎包含了所有的齒面數據點,但是不能避免錯誤對應點的產生,導致最終結果稍有偏移;而在權重為70%時, 有效避免了錯誤對應點的產生,使齒面測量數據補償結果更精準。
如圖11所示,將各算法在不同權重下的最終結果進行比較。由圖可知,各算法在權重為40%時,最大誤差及誤差補償率都較差,這是由于在權重為40%時, 選取的點不足以顯示全齒面的數據特征,導致一些齒面點的誤差不能進行精細的補償。而在權重為70%和90%時,各算法的最大誤差及誤差補償率相差不大,但70%更佳,這是由于在權重為90%時,雖然幾乎包含了所有的齒面數據點,但是不能避免錯誤對應點的產生,導致最終結果稍有偏移;而在權重為70%時, 有效避免了錯誤對應點的產生,使齒面測量數據補償結果更精準。
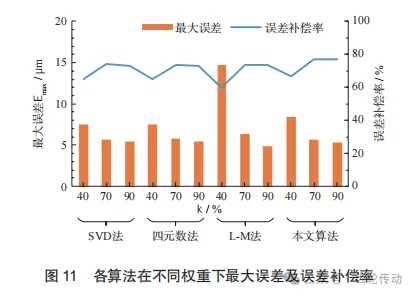 為比較最優權重下各算法對應點的誤差補償效果, 將各算法的全部齒面測量點的誤差補償率繪出,如圖12所示。由圖可得,4種算法整體趨勢大致相同, 且第15—第18點的誤差補償率都偏低,這是由于第15—第18點的原始誤差(圖9)本身比較小,隨著齒面整體旋轉配準,此處誤差呈現出放大現象。本文算法與其他3種算法相比起伏較小,且整體誤差補償率較高,證明了本文算法相比于其他3種算法有更高的求解精度。
為比較最優權重下各算法對應點的誤差補償效果, 將各算法的全部齒面測量點的誤差補償率繪出,如圖12所示。由圖可得,4種算法整體趨勢大致相同, 且第15—第18點的誤差補償率都偏低,這是由于第15—第18點的原始誤差(圖9)本身比較小,隨著齒面整體旋轉配準,此處誤差呈現出放大現象。本文算法與其他3種算法相比起伏較小,且整體誤差補償率較高,證明了本文算法相比于其他3種算法有更高的求解精度。
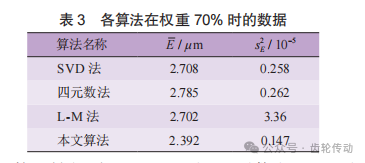
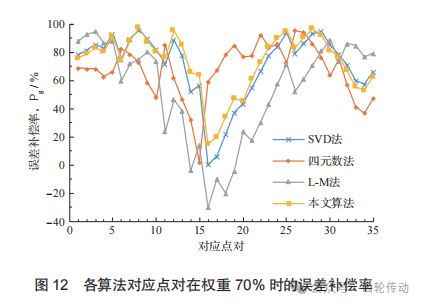 為了進一步比較各算法在最優權重下的補償效果,將各算法在權重70%時最終補償后的的平均誤差
為了進一步比較各算法在最優權重下的補償效果,將各算法在權重70%時最終補償后的的平均誤差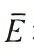 和方差s2E計算出,如表3所示。由表可得,本文算法在權重70%補償后的平均誤差
和方差s2E計算出,如表3所示。由表可得,本文算法在權重70%補償后的平均誤差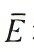 為2.392μm,方差s2E為0.147,皆小于其他算法。
為2.392μm,方差s2E為0.147,皆小于其他算法。
 綜上所述,相比于SVD法、四元數法和L-M法,本文算法在實際測量中求解精度高、穩定性好,驗證了其在實際應用中的可行性與有效性。
綜上所述,相比于SVD法、四元數法和L-M法,本文算法在實際測量中求解精度高、穩定性好,驗證了其在實際應用中的可行性與有效性。
為提升汽車的安全與節能性能,本文針對汽車驅動橋螺旋錐齒輪實測齒面和理論齒面存在的測量誤差, 提出了一種基于對偶四元數優化的迭代最近點 (ICP) 齒面測量誤差補償法,利用對偶四元數對齒面配準模型進行表示并使用凸松弛的全局優化算法對旋轉矩陣進行優化。由螺旋錐齒輪實際測量實驗結果可知,齒輪凹齒面的誤差補償率達77%,最大誤差由補償前的22.11μm降至5.64μm,平均誤差由補償前的10.34μm降至2.38μm。相比于傳統奇異值分解法(SVD)、四元數法和Levenberg-Marquardt(L-M)法,本文算法補償精度和穩定性更高,驗證了所提補償方法的可行性。
參考文獻略.
各位粉絲朋友們,歡迎閱讀本期小編推送的《汽車驅動橋螺旋錐齒輪齒面測量誤差補償方法》文章。文章主要介紹了提升汽車驅動橋螺旋錐齒輪齒面加工質量對整車的安全與節能性能有重要意義。
該文針對汽車驅動橋螺旋錐齒輪實測和理論齒面存在的測量誤差,提出了一種基于對偶四元數優化的迭代最近點(ICP)齒面測量誤差補償方法。
本篇文章因篇幅較長,特安排兩期推送,本期推出文章最后剩余內容。
本期推出:汽車驅動橋螺旋錐齒輪齒面測量誤差補償方法(二)
4實測結果與分析
為了驗證本文算法的補償效果,使用如圖6所示HyB-35型齒輪測量機對汽車驅動橋螺旋錐齒輪齒面進行點接觸式測量。













5結論
為提升汽車的安全與節能性能,本文針對汽車驅動橋螺旋錐齒輪實測齒面和理論齒面存在的測量誤差, 提出了一種基于對偶四元數優化的迭代最近點 (ICP) 齒面測量誤差補償法,利用對偶四元數對齒面配準模型進行表示并使用凸松弛的全局優化算法對旋轉矩陣進行優化。由螺旋錐齒輪實際測量實驗結果可知,齒輪凹齒面的誤差補償率達77%,最大誤差由補償前的22.11μm降至5.64μm,平均誤差由補償前的10.34μm降至2.38μm。相比于傳統奇異值分解法(SVD)、四元數法和Levenberg-Marquardt(L-M)法,本文算法補償精度和穩定性更高,驗證了所提補償方法的可行性。
參考文獻略.
